Sen(Qian)’s Memo

https://openreview.net/forum?id=wfgZc3IMqo

今までの損失関数修正とラベル修正を組み合わせた。その上、回帰問題とみなすことで、shifted Gaussian Label Noise Modelの知見を応用したらしい。

古典的な手法(2019以前？)のデータ、損失、ラベルに対してそれぞれ変換を施す手法は次のSurveyにある。

📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future

損失関数変換: Noisyなラベルの損失への寄与を減らす。学習の初期では有効だが、正しいラベルが大体訓練された後に、結局Noisy Labelがgradientの主なものを占めて、そこから性能が下がり続けてしまう。だが、学習が有意義であるepochを増やせる。

ラベル変換: Noisyなラベルを正しいと思われるものに変換すること。識別器の判断結果に基づいてRe-labelingするが、

• あまりに早い段階だと識別器自体の訓練が未熟で、正しくRe-labelingできない。
• あまりに遅い段階だと識別器自体がノイズをも記憶してしまい、正しくRe-labelingできない。

この2つを組み合わせてみたよ。つまり、損失関数変換で有効な訓練Epochを引き延ばし、その間で十分にRe-labelingをしてもらうという算段。

後は、分類問題を回帰問題に変換して解いているらしい。

Wikipedia:

Compositional data - Wikipedia

https://en.wikipedia.org

意味としては、加算(pertubation)、累乗、内積などを定義している空間である。

$D$次元のVector$\mathbf{p} = (p_1, \cdots, p_D)^T$について、すべての成分が非負で、和が$\sum_{i=1}^D p_i = 1$である。実質的にVectorは$D-1$次元であるし、和が固定されているVectorである。

組成データは定義の通りに、制限がかかっているデータであるので、通常の統計的な手法を使用することはできない。

そのままデータの関係性があって、統計的なテク=正規化とかが使えない。何かしらの数学的な変換を施すことで正規化ができるような通常のデータに変換したいというのがモチベ。

ちなみにモチベとしては、Labelの各成分の和が必ず1になるので、それって組成データじゃないか！？ということ。

組成データの各組成の相関情報には、何倍かという量が重要。それを扱うのに

1. log比変換で組成データを扱うことで、制限がない普通のデータと同じように見なす。
2. 通常の統計的なテクニックを使い、変換した後のデータを見る。
3. 逆変換を行って、組成データの世界に戻す。

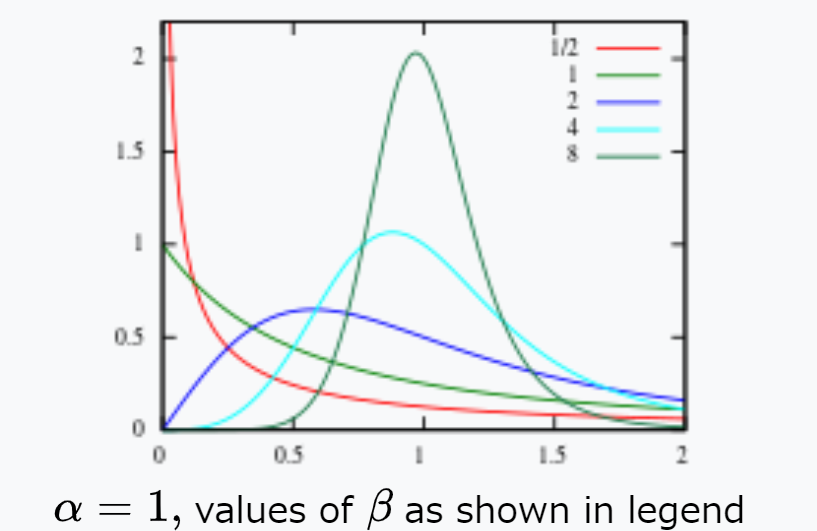
という流れを提示した。特に組成データの統計モデリングは変換されたデータがLogistic Normal Distributionとなることを仮定している。以下の形の分布らしい。

組成データから制限がないような空間に変換するのはいろいろあるが、この論文ではlogによる変換に着目する。

Wikipedia:

Compositional data - Wikipedia

https://en.wikipedia.org

以下のように、例えば最後の要素との比を計算し、対数をとる。割る要素は最後のものではなくてもよく、適当に選べばよい。ただ、非対称性=どのデータを選んだのかによって変換先が結構違ってくる、を持ってしまう。分布が非対称だと、うまく正規化できない。

$gm()$は相乗平均である。

計算を進めてlogをほどくと、以下のようになり、和が0になるという素晴らしい性質がある。つまり変換先も$D-1$次元であるといえる(和が0という制約が残るので)。なので、$\mathbb{R}^D$とあるが線形空間として同型なのは$\mathbb{R}^{D-1}$なのが内実。

そのうえ、幾何平均なので、どのデータを選ぶも何もなく、対称性を持つ。

以下のように、最後の要素との比を計算し、対数をとる。$V$は$D$次元の直交基底から$D-1$本選んで。$D \times (D-1)$の行列で、基底変換をしている。これによって、clrで同型でしかなかった線形空間にちゃんと写像できるようになった。

直交基底はグラムシュミットの直交化法でもよいし、幾何的統計的な特徴を考慮して作ってもよい。

全体の流れとしては、

1. Label Smoothingを使って、普通のデータを組成データに変換する。

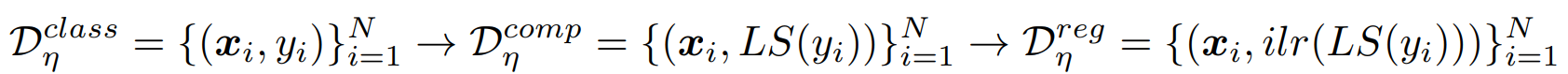
1. $D_{\eta}^{reg}$は回帰に使うデータセットなので、回帰を計算する。ここで、ReweightingとLoss Correctionを両方使った手法にする。
2. 回帰の計算結果を、もともとのクラスに戻す。

まずはLabel Smoothingを行うことによって、one-hotのラベル$\delta_y \in \Delta^{K-1}$を$1/K$が平均で分散が1の成分で構成された$\mathbf{u} \in \mathbb{R}^K$と混合させる。ここで、$\Delta^{K-1}$と表記したのは、ラベルのone-hotベクトルを組成データとみなしているから。$\gamma$を用いて、以下のようにする。

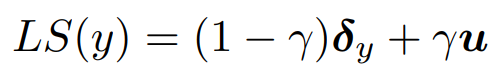
ilr変換を施しているが、行列$V \in \mathbb{R} ^ {K \times (K-1)}$は、以下のHelmert行列である。

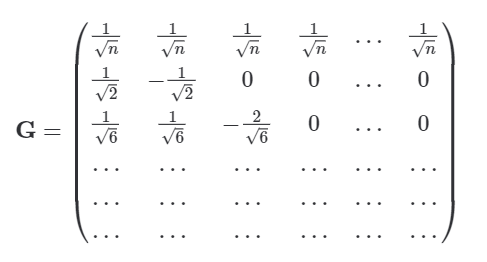
参考: https://www.hello-statisticians.com/explain-terms-cat/helmert1.html#Helmert

1行目はすべて$1/\sqrt{n}$である。2行目以降は、$k$行目ならば$k-1$個の$1/\sqrt{k(k+1)}$が続き、最後には$-(k-1)/\sqrt{k(k+1)}$となる。

使うメリットとしては、計算が簡単、幾何学的な特性やパターンを保持するがノイズを排除しやすい。

これで、$ilr(\mathbf{x}) = V ^ T clr(\mathbf{x})$となり、$\mathbb{R}^{K-1}$のベクトルを得られた。

ノイズがあるデータ$t(x)=\mu(x)+\epsilon(x)$について、ガウシアンノイズに従うという仮定の下で、最尤推定で$\mu_\theta, \sigma_{\theta}^2$を得る。この推定自体をDNNでやったらしい。今までは離散的に扱われていたので、このように連続値のNoiseを足すモデルはなかった。

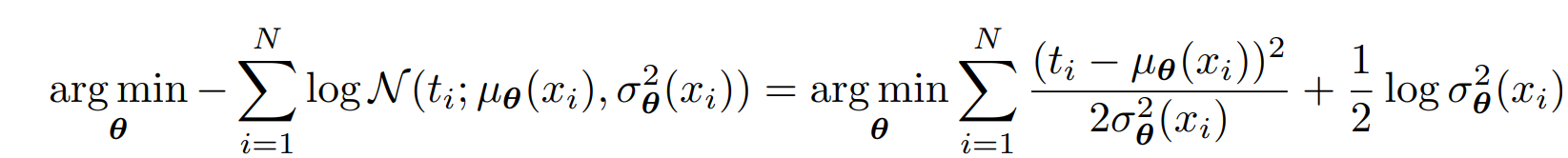
この学習において、シグマの中では各データについて、$1/2\sigma_{\theta}^2$でReweightingしているといえる(各データごとに軽重をつけているわけではない！)

また、ガウス尤度モデルだと自動で2項目で正則化のような役割を果たすこともできる。

この分布を推定する操作をLoss Reweightingと定義している。なんか、伝統的なReweightingと違くね？？？

だが、Noisyな環境ではそれだけでは足りないのが現状。そこで、Shifted Noise Modelを提案する。$\mu$が真のラベルで、観測されるのは$t$。その間のシフトである$\Delta = t - \mu$を考慮しなければならない。

この$\Delta$を直接推定するのは難しい(それはそう)。代わりに、前に学習したNetworkの重みの指数移動平均=EMAをとることで、変な方向行ってもある程度抑えられるようにさせている。これは先行研究にもあったそのもの。

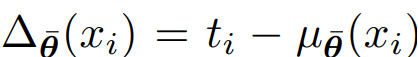
$\bar{\theta}$は指数移動平均。つまり学習の式は以下の通り。モデルの指数移動平均版の予測する期待値と、今時点の期待値とのMSEをとる。本来は与えられたNoisyなラベルの位置にあたるものが指数移動平均版の予測する期待値だった。

ただしこの手法では、学習の早い段階ではwarm-upとして、$t = \mu + (1 - \alpha^e) \Delta$である。$\alpha$は1に近く、$e$はエポック。エポックが大きくなるほど、本来の$t = \mu + \Delta$の式に近づくが、もともとの式では最初では与えられたNoisyなラベルの$t$のままにしてる。

ここまで訓練したことで、分類→回帰で何かしらの予測をすることができた。最後は分類に戻す必要がある。

人工的なノイズの混入は対称的なものと非対称的なもの。4割間違うCIFAR-10とかでも高い性能向上が見られた。

再ラベル付けによる正確性は高レベルな対称ノイズには無力だが、低レベルの対称ノイズではいい結果を挙げている。それでも、対称ノイズに対してロバストな実験結果になっている。